Cos'è un grafo?
Sempre di più il nostro mondo è caratterizzato da una fitta rete di relazioni e connessioni. La teoria dei grafi studia queste interazioni, rappresentandole con strutture composte da nodi collegati da archi, chiamate grafi. La struttura e la costruzione dei grafi sono la chiave per comprendere il mondo complesso che ci circonda. Questa disciplina ci aiuta a comprendere e analizzare sistemi complessi in vari campi, dalle reti sociali alle infrastrutture tecnologiche.
Esplorando questo campo, è possibile comprendere come le connessioni influenzano comportamenti, come le informazioni si diffondono attraverso le reti e come le strutture complesse possono essere semplificate e analizzate. La teoria dei grafi, quindi, non solo fornisce una mappa per decifrare le connessioni, ma offre anche gli strumenti per ottimizzare, prevedere e influenzare i comportamenti all'interno di queste reti.
Tipologie di grafi
Esistono molti tipi di grafi, ciascuno con caratteristiche e applicazioni specifiche. Ogni tipologia è fondamentale per una vasta gamma di applicazioni, dalle reti sociali e mappe stradali, fino alla progettazione di circuiti e modelli economici. Conoscere queste strutture significa comprendere meglio il mondo che ci circonda. In questa sezione, esploreremo alcune tra le tipologie di grafi più importanti e utilizzate.
Grafi semplici
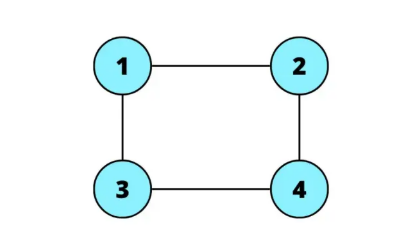
Non contengono archi multipli né loop. Sono la rappresentazione più basilare e comune dei grafi, spesso utilizzati in reti sociali e modelli base.
Caratteristiche:
- Gli archi non hanno direzione.
- Ogni coppia di nodi può essere collegata al massimo da un solo arco.
- Adatti per rappresentare relazioni simmetriche, come amicizie in una rete sociale.
Un gruppo di amici in una rete sociale: ogni nodo rappresenta una persona e un arco rappresenta un'amicizia reciproca.
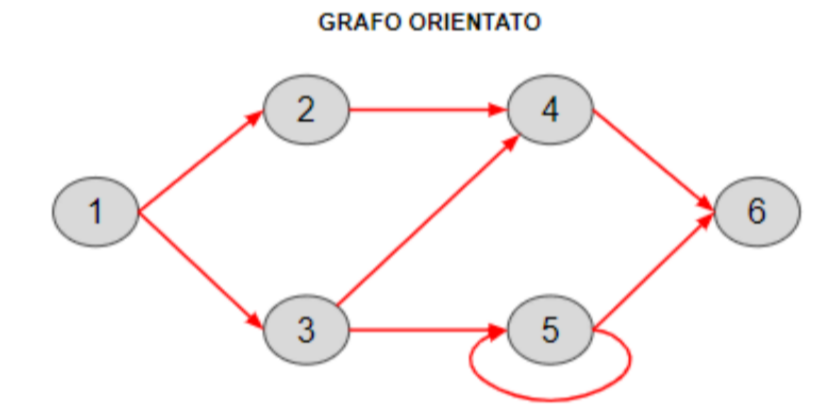
Grafi orientati
Nei grafi orientati, ogni arco ha una direzione, rappresentata da una freccia.
Caratteristiche:
- Gli archi sono direzionali, quindi un arco (𝐴,𝐵) è diverso da (𝐵,𝐴).
- Usati per rappresentare relazioni non simmetriche.
Reti stradali a senso unico: un arco da 𝐴 a 𝐵 rappresenta una strada percorribile solo in quella direzione.
Strutture gerarchiche, come alberi genealogici o organigrammi aziendali.
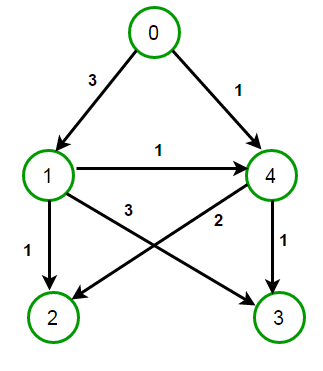
Grafi ponderati
Nei grafi ponderati ogni arco ha un peso associato che può rappresentare distanza, costo, tempo o altre metriche.
Caratteristiche:
- I pesi sono numerici e possono essere positivi, negativi o nulli.
- Essenziali per algoritmi di ottimizzazione come Dijkstra o A*.
Calcolo del percorso più breve in una mappa stradale (es. Google Maps).
Reti di comunicazione, per ottimizzare il trasferimento dati tra due dispositivi.
Grafi planari
Possono essere disegnati su un piano senza che i loro archi si intersechino, eccetto nei vertici.
Caratteristiche:
- Hanno applicazioni in topologia e geometria.
- Sono studiati per la loro semplicità e chiarezza visiva.
Reti di trasporto urbano (es. mappe delle metropolitane).
Layout di circuiti elettronici per evitare interferenze tra connessioni.
Applicazioni semplici

(famiglia, amicizie, partner)
Reti sociali
La teoria dei grafi è utilizzata per modellare le reti sociali umane, dove i nodi rappresentano individui e gli archi rappresentano relazioni come amicizie, parentela o interazioni. Studiando queste reti, è possibile identificare i legami più forti o deboli e comprendere la struttura delle comunità. Ad esempio, si possono analizzare fenomeni come la diffusione di idee o emozioni all'interno di un gruppo. Questa applicazione è utile anche in sociologia e psicologia per studiare come le relazioni personali influenzano il comportamento e il benessere degli individui.
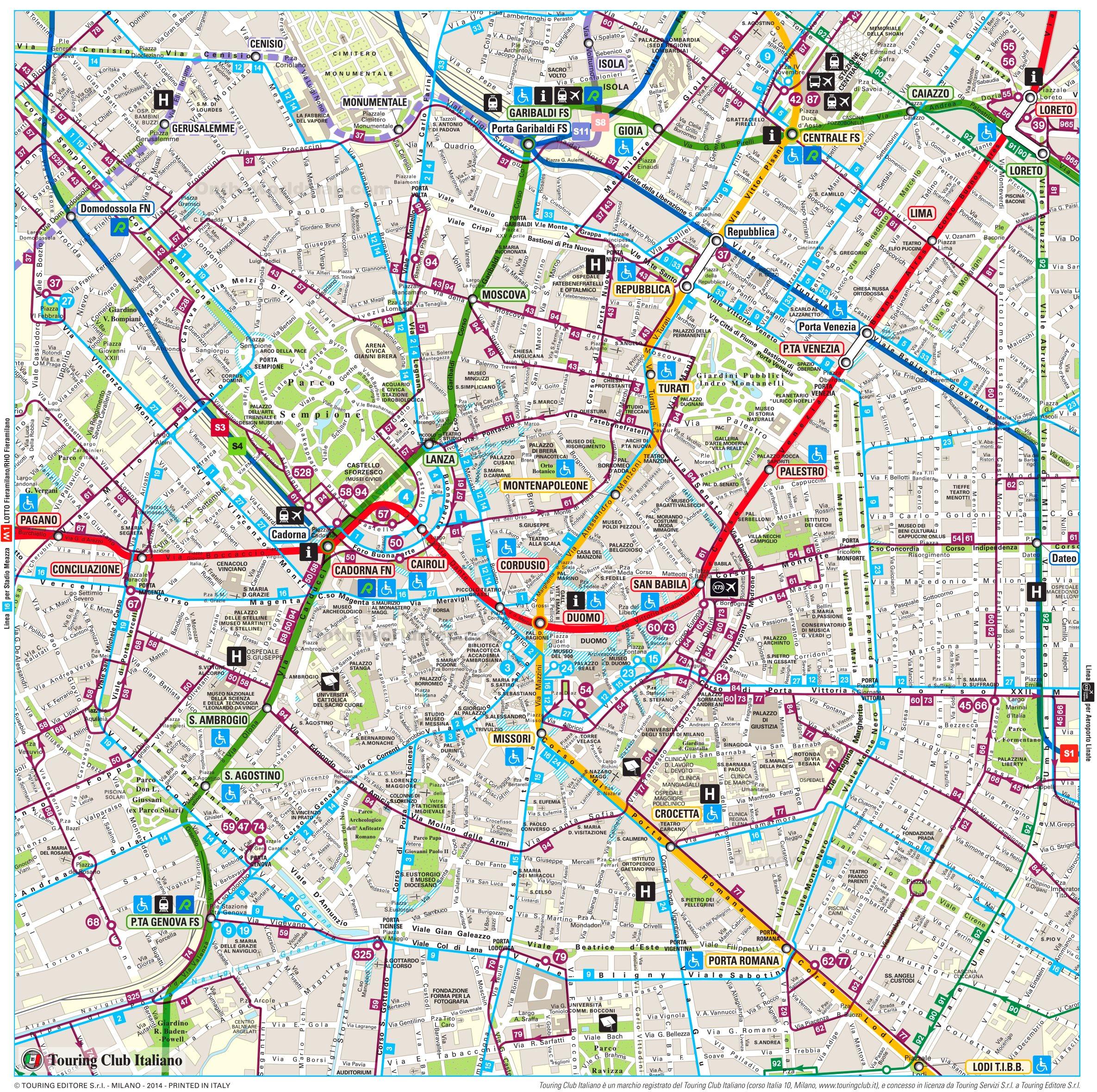
Mappe stradali
I grafi sono utilizzati per rappresentare reti stradali, dove i nodi sono incroci o punti di interesse e gli archi rappresentano strade o percorsi. Ogni arco può essere associato a un peso, come la lunghezza, il tempo di percorrenza o il traffico. Questo modello permette di calcolare il percorso più breve o più veloce tra due punti utilizzando algoritmi come Dijkstra o A*. Applicazioni come Google Maps e Waze sfruttano i grafi per offrire itinerari ottimizzati agli utenti. Inoltre, i grafi sono fondamentali nella pianificazione logistica e nella gestione dei trasporti pubblici.

raccomandazione Amazon
Shopping online e raccomandazioni
I sistemi di raccomandazione nei siti di shopping online si basano sui grafi per analizzare le relazioni tra utenti, prodotti e preferenze. Gli utenti sono rappresentati come nodi, con archi che li collegano agli articoli che hanno visualizzato, acquistato o recensito. Questo approccio consente di suggerire prodotti simili o popolari, migliorando l'esperienza dell'utente e aumentando le vendite. Ad esempio, Amazon utilizza grafi per proporre articoli sotto la sezione "chi ha comprato questo, ha comprato anche" (Amazon Personalize).
I grafi permettono anche di analizzare il comportamento degli utenti per ottimizzare le campagne pubblicitarie.
Economia e finanza
Nell'economia e nella finanza i grafi vengono utilizzati per rappresentare reti di transazioni, mercati e relazioni tra aziende. I nodi possono rappresentare individui, istituzioni o azioni, mentre gli archi mostrano flussi di denaro, scambi o investimenti.
Questa rappresentazione aiuta a identificare i principali attori di un mercato e a monitorare le interazioni economiche globali. Ad esempio, i grafi sono utilizzati per analizzare il rischio sistemico nei mercati finanziari e prevedere crisi economiche. Inoltre, trovano applicazione nella tecnologia blockchain dove le reti di transazioni e le relazioni tra i nodi possono essere modellate per garantire trasparenza, tracciabilità e sicurezza nelle operazioni economiche.